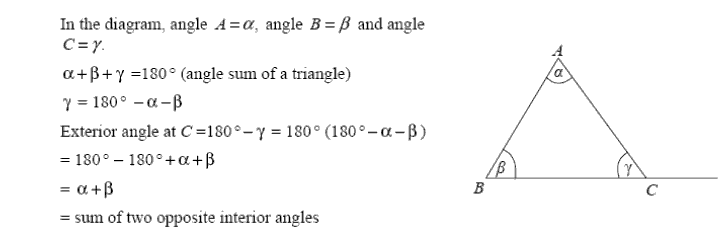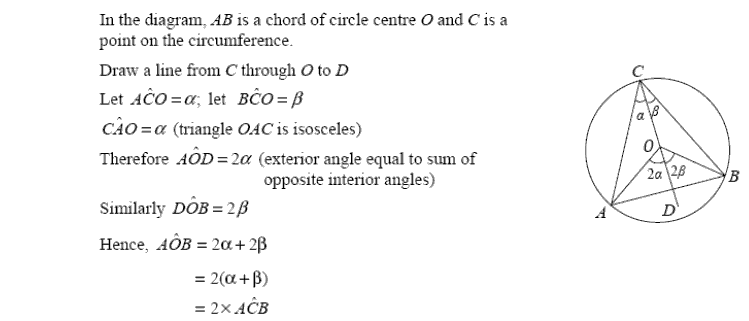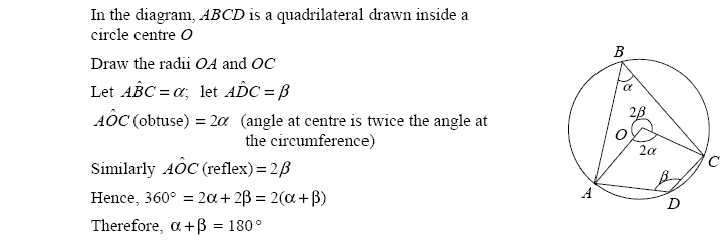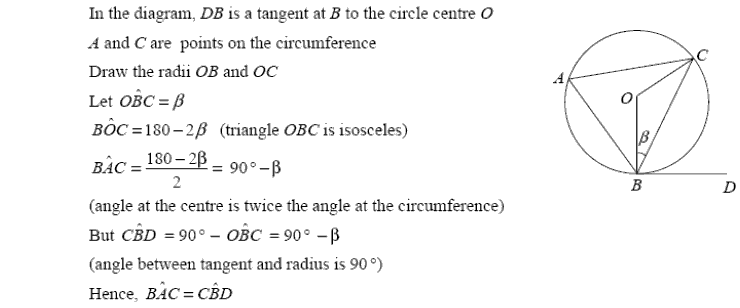Topic: Circle Theorems; Geometrical Proof (Higher - Unit 3)
| Specification References: G2.3 G2.3 Justify simple geometrical properties. Simple geometrical proofs. |
Candidates should be able to:
- apply mathematical reasoning, explaining and justifying inferences and deductions
- show step-by-step deduction in solving a geometrical problem
- state constraints and give starting points when making deductions
Notes
Candidates should be able to explain reasons using words or diagrams.
Candidates should realise when an answer is inappropriate.
On Higher tier, proofs involving congruent triangles and circle theorems may be set.
Questions assessing quality of written communication will be set that require clear and logical steps to be shown, with reasons given.
Mini-investigations will not be set but candidates will be expected to make decisions and use the appropriate techniques to solve a problem drawing on well-known facts, such as the sum of angles in a triangle.
Multi-step problems will be set.
Redundant information may sometimes be used, for example the slant height of a parallelogram. Candidates should be able to identify which information given is needed to solve the given problem.
Examples
- Proof that the angle subtended by a chord at the centre of a circle is twice the angle subtended at the circumference in the same segment:

view more examples